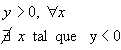quinta-feira, 19 de dezembro de 2013
variaçao do sinal da funçao quadratica
Estudar o sinal de uma função, é determinar para quais valores reais de x a função é positiva, negativa ou nula. A melhor maneira de se fazer isso, é através do gráfico, pois permite-nos uma avaliação mais ampla da situação.
A parábola pode tocar o eixo horizontal duas vezes, uma só vez ou não tocar esse eixo. Tudo depende das raízes da equação y = ax2 + bx + c.

26 - Seja a equação ax2+bx+c = 0. Dividindo ambos os membros por a≠0, vem:
x2 + (b/a)x + (c/a) = 0, Sendo x1 e x2 as raízes, temos as seguintes fórmulas para a soma S e o produto P das raízes: S = x1 + x2 = -b/a e P = x1 . x2 = c/a. Ora, poderemos escrever então: S = -b /a => -S = b/a. Substituindo os valores de b/a e c/a na equação acima, vem finalmente: x2 – Sx + P = 0, que é a forma (S,P) da equação do 2º grau.
Esta maneira de apresentar a equação do 2º grau é bastante conveniente, uma vez que permite conhecer a soma das raízes e o produto das raízes, sem resolver a equação. Este fato, facilita até a solução mental da equação, sem aplicação da fórmula de Bhaskara.
x2 + (b/a)x + (c/a) = 0, Sendo x1 e x2 as raízes, temos as seguintes fórmulas para a soma S e o produto P das raízes: S = x1 + x2 = -b/a e P = x1 . x2 = c/a. Ora, poderemos escrever então: S = -b /a => -S = b/a. Substituindo os valores de b/a e c/a na equação acima, vem finalmente: x2 – Sx + P = 0, que é a forma (S,P) da equação do 2º grau.
Esta maneira de apresentar a equação do 2º grau é bastante conveniente, uma vez que permite conhecer a soma das raízes e o produto das raízes, sem resolver a equação. Este fato, facilita até a solução mental da equação, sem aplicação da fórmula de Bhaskara.
Exemplos: Verifique, mentalmente, as raízes das equações abaixo:
a) x2 – 5x + 6 = 0
Soma das raízes = S = 5 e Produto das raízes = P = 6
Ora, os números que somados dá 5 e multiplicados dá 6, são 2 e 3 que são as raízes da equação.
Soma das raízes = S = 5 e Produto das raízes = P = 6
Ora, os números que somados dá 5 e multiplicados dá 6, são 2 e 3 que são as raízes da equação.
b) x2 – x – 12 = 0
S = 1 e P = -12. Os números que somados é igual 1 e multiplicados dá - 12 são: 4 e –3.
c) x2 +3x - 4 = 0
S = - 3 e P = -4. Então: as raízes da equação são, –4 e 1.
S = - 3 e P = -4. Então: as raízes da equação são, –4 e 1.
d) x2 + x - 999000 = 0
S = -1 e P = -999000. Então: as raízes são, -1000 e 999.
S = -1 e P = -999000. Então: as raízes são, -1000 e 999.
e) x2 – (1+ √3)x + √3 = 0. R: as raízes são, 1 e √3.
Com a forma (S,P) da equação do 2º grau [x2 – Sx + P=0], podemos resolver o problema inverso da determinação das raízes, ou seja, compor a equação cujas raízes são conhecidas.
Exemplo 1: Qual a equação do 2º grau cujas raízes são 10 e 78?
Temos: S = 10+78 = 88 e P = 10.78 = 780
Logo, a equação é: x2 – 88x + 780 = 0.
Exemplo 2: Qual a equação cujas raízes são -4 e 100?
Temos: S = -4 + 100 = 96 e P = -4(100) = -400
Logo, a equação procurada é x2 - 96x – 400 = 0.
Temos: S = -4 + 100 = 96 e P = -4(100) = -400
Logo, a equação procurada é x2 - 96x – 400 = 0.
Exemplo 3: Qual a equação cujas raízes são w -1 e w+1?
Temos: S = w –1 + w + 1 = 2w => P = (w –1)(w+1) = w2-1
Logo, a equação procurada é: x2 – 2wx + w2 – 1 = 0.
Temos: S = w –1 + w + 1 = 2w => P = (w –1)(w+1) = w2-1
Logo, a equação procurada é: x2 – 2wx + w2 – 1 = 0.
Agora resolva, mentalmente, a equação x2 + 100x – 60000 = 0. R: -300 e 200.
27 - Exercícios Resolvidos
1 – [Ucsal] – Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o ponto (-1, 8) pertence ao gráfico dessa função, então:
a) o seu valor máximo é 1,25
b) o seu valor mínimo é 1,25
c) o seu valor máximo é 0,25
d) o seu valor mínimo é 12,5
d) o seu valor mínimo é 12,5
e) o seu valor máximo é 12,5.
Solução: Sabemos que a função quadrática pode ser escrita na forma fatorada: y = a(x - x1)(x - x2), onde x1 e x2, são os zeros ou raízes da função. Portanto, poderemos escrever: y= a [x -(- 2)](x - 3)= a(x + 2)(x – 3) => y = a(x + 2)(x – 3) => 8 = a(-1 + 2)(-1 – 3) => 8= a (1)(-4) = 4. Daí vem: a = -2. A função é, então: y = -2(x + 2) (x - 3), ou y = (-2x -4) (x – 3) => y = -2x2 + 6x - 4x + 12 => y = -2x2 + 2x + 12. Temos então: a = -2, b = 2 e c = 12.
Como a é negativo, concluímos que a função possui um valor máximo. Isto já elimina as alternativas B e D. Vamos então, calcular o Vmáx da função:
? = b2-4ac = 22-4.(-2).12 = 4+96 = 100. Portanto, yv = - 100/4(-2) = 100/8 = 12,5
2 – Que número excede o seu quadrado o máximo possível?
a) 1/2 b) 2 c) 1 d) 4 e) -1/2
a) 1/2 b) 2 c) 1 d) 4 e) -1/2
Solução: Seja x o número procurado. O quadrado de x é x2.O número x excede o seu quadrado, logo: x - x2. Ora, a expressão anterior é uma função quadrática y = x - x2. Podemos escrever: y = - x2 + x onde a = -1, b = 1 e c = 0. O valor procurado de x, será o xv (abcissa do vértice da função). Assim, xv = - b/2.a = -1/2(-1) = 1/2. Logo, a alternativa correta é a letra A.
3 – Se f(x) = 1/[x(x+1)] com x≠0 e x≠-1, então o valor de S = f(1) + f(2) + f(3) + ... + f(100) é:
a)100 b) 101 c) 100/101
d) 101/100 e) 1
Solução: Temos: f(x) = 1/[x(x+1)] = (1/x) – 1/(x+1). Portanto:
f(1) = 1/1 - 1/2
f(2) = 1/2 - 1/3
f(3) = 1/3 - 1/4
f(4) = 1/4 - 1/5
f(5) = 1/5 - 1/6.... f(99) = 1/99 - 1/100.
f(1) = 1/1 - 1/2
f(2) = 1/2 - 1/3
f(3) = 1/3 - 1/4
f(4) = 1/4 - 1/5
f(5) = 1/5 - 1/6.... f(99) = 1/99 - 1/100.
f(100) = 1/100 - 1/101.
Somando membro a membro as igualdades acima (observe que os termos simétricos se anulam entre si), vem: f(1) + f(2) + f(3) + ... + f(100) = 1 - 1/101 = 100/101.
4 – Ucsal – Sejam f e g funções de R em R, sendo R o conjunto dos números reais, dadas por f(x) = 2x - 3 e f(g(x)) = -4x + 1. Nestas condições, g(-1) é igual a:
a) –5 b) –4 c) 0 d) 4 e) 5
Solução: Como f(x) = 2x -3, podemos escrever: f[g(x)] = 2.g(x) - 3 = - 4x + 1
Logo, 2.g(x) = - 4x +4 => g(x) = -2x + 2. Assim, g(-1) = -2(-1) + 2 = 4.
Logo, 2.g(x) = - 4x +4 => g(x) = -2x + 2. Assim, g(-1) = -2(-1) + 2 = 4.
5 - O conjunto imagem da função y = 1 / (x - 1) é o conjunto:
a) R - { 1 } b) [0,2] c) R - {0} d) [0,2) e) (-2 ,2]
Solução: Se y = 1 / (x - 1), então x - 1 = 1 / y. Como o conjunto imagem é o conjunto dos valores de y, percebemos que y não pode ser nulo, pois não existe divisão por zero. Logo, R - {0}.
6 - Determine o domínio da função y = (x+1) / (x - 2). Solução: Como não existe divisão por zero, vem imediatamente que: x - 2 ≠ 0 <=> x≠2. Logo, o domínio da função será D = R - {2}, onde R é o conjunto dos números reais.
7 – Seja f uma função tal que f(n + 1) = [(2.f(n) + 1)] / 2 para todo n inteiro positivo ef(1) = 2. Nestas condições, o valor de f(101) é:
(a) 102 (b) 101 (c) 86 (d) 76 (e) 52
Solução: Teremos, fazendo n = 1,2,3 4,... na expressão f(n+1) = [(2.f(n)+1)/2:
n = 1 ? f(1 + 1) = f(2) = [2.f(1) + 1] / 2 = [2.2 + 1] / 2 = 5 / 2
n = 2 ? f(2 + 1) = f(3) = [2.f(2) + 1] / 2 = [2.(5 / 2) + 1] / 2 = 3
n = 3 ? f(3 + 1) = f(4) = [2.f(3) + 1] / 2 = [2.3 + 1] / 2 = 7 / 2
n = 4 ? f(4 + 1) = f(5) = [2.f(4) + 1] / 2 = [2.(7 / 2) + 1] / 2 = 4
...........................................................................................................
Vamos resumir os valores obtidos acima:
f(1) = 2 = 4 / 2
f(2) = 5 / 2
f(3) = 3 = 6 / 2
f(4) = 7 / 2
f(5) = 4 = 8 / 2
….........................................................................................................
Observe que o denominador é sempre 2 e o numerador é o valor de n acrescido de 3 unidades, pois:
f(1) = 4 / 2 e 4 = 1 + 3
f(2) = 5 / 2 e 5 = 2 + 3
f(3) = 6 / 2 e 6 = 3 + 3
f(4) = 7 / 2 e 7 = 4 + 3
f(5) = 8 / 2 e 8 = 5 + 3
f(1) = 4 / 2 e 4 = 1 + 3
f(2) = 5 / 2 e 5 = 2 + 3
f(3) = 6 / 2 e 6 = 3 + 3
f(4) = 7 / 2 e 7 = 4 + 3
f(5) = 8 / 2 e 8 = 5 + 3
…........................................................................................................
Observe que a lei de formação para um n inteiro positivo qualquer será então f(n) = (n + 3)/2
Portanto, o valor de f(101) será obtido fazendo n = 101, o que resulta:
f(101) = (101 + 3) / 2 = 104 / 2 = 52
Observe que a lei de formação para um n inteiro positivo qualquer será então f(n) = (n + 3)/2
Portanto, o valor de f(101) será obtido fazendo n = 101, o que resulta:
f(101) = (101 + 3) / 2 = 104 / 2 = 52
27 – Exercícios Propostos
1 – Seja f uma função tal que f(n + 1) = [(2.f(n) + 1)] / 2 para todo n inteiro positivo e f(1) = 2. Nestas condições, determine o valor de f(105) + f(109).Resposta: 110
2 – [PUC] Se f é uma função tal que f(1) = a, f(?) = b e f(x + y) = f(x) . f(y), ? x, y ? R, então f(2 + ?) é igual a:
a) a b) b c) a2b d) ab2 e) a + b
3 – [UFBA] Se f (g (x) ) = 5x - 2 e f (x) = 5x + 4 , então g(x) é igual a:
a) x – 2 b) x – 6 *c) x - 6/5 d) 5x - 2 e) 5x + 2
a) x – 2 b) x – 6 *c) x - 6/5 d) 5x - 2 e) 5x + 2
4 - A função f é tal que f(2x + 3) = 3x + 2. Nestas condições, f(3x + 2) é igual a:
a) 2x + 3 b) 3x + 2 c) (2x + 3) / 2 *d) (9x + 1) /2 e) (9x - 1) / 3
a) 2x + 3 b) 3x + 2 c) (2x + 3) / 2 *d) (9x + 1) /2 e) (9x - 1) / 3
5 – Qual o domínio da função y = (x - 4)1/4? Resp: D = [4, +? ).
6 – Qual o conjunto imagem da função y = 1/x? Resp: Im = R – {0}.
7 – Qual o domínio da função y = (senx)/x? Resp: D = R – {0}.
8 – Sendo f(x) = senx e g(x) = logx, pede-se determinar o valor de g[f(? /2)]. Resp: 0
9 - Seja f uma função definida para todo x real, satisfazendo as condições:
f(3) = 2 e f(x+3) = f(x).f(3)
10 – Dadas as funções f(x)= 4x + 5 e g(x) =2x - 5k, ocorrerá gof(x)= fog(x) se e somente se k for igual a:
a) -1/3 b) 1/3 c) 0 d) 1 e) –1
11 – A diferença entre dois números é 8. Para que o produto seja o menor possível, um deles deve ser:
a) 16 b) 8 c) 4 d) –4 e) -16
12 - A diferença entre dois números é 8. O menor valor que se pode obter para o produto é:
a) 16 b) 8 c) 4 d) –4 e) –16
13 – A função f é definida por f(x) = ax + b. Sabe-se que f(-1) = 3 e f(3) = 1, então podemos afirmar que f(1) é igual a:
a) 2 b) –2 c) 0 d) 3 e) –3
questões de função quadratica
Questão 1
Calcule o valor de k de modo que a função f(x) = 4ax² – 4x – k não tenha raízes, isto é, o gráfico da parábola não possui ponto em comum com o eixo x.
Questão 2
Determine os valores de p, para que a função f(x) = (m – 2)x² – 2x + 6 admita raízes reais.
Questão 3
O gráfico da função quadrática definida por y = x² – mx + (m – 1), em que m Є R, tem um único ponto em comum com o eixo das abscissas. Determine y associado ao valor de x = 2.
Questão 4
Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abscissas.
Respostas
Resposta Questão 1
∆ < 0
b² – 4ac < 0
(–4)² – 4 * 4 * (–k) < 0
16 + 16k < 0
16k < – 16
k < –1
O valor de k para que a função não tenha raízes reais deve ser menor que – 1.
Resposta Questão 2
Para essa situação temos que ∆ ≥ 0.
∆ ≥ 0
b² – 4ac ≥ 0
(–2)² – 4 * (m – 2) * 6 ≥ 0
4 – 4 * (6m – 12) ≥ 0
4 – 24m + 48 ≥ 0
– 24m ≥ – 48 – 4
– 24m ≥ – 52
24m ≤ 52
m ≤ 52/24
m ≤ 13/6
O valor de m que satisfaça a condição exigida é m ≤ 13/6.
Resposta Questão 3
Um ponto em comum significa dizer uma única raiz, então ∆ = 0.
y = x² – mx + (m – 1)
Substituir m = 2, no intuito de obter a lei da função
y = x² – 2x + (2 – 1)
y = x² – 2x +1
Substituindo x = 2, para determinarmos o valor de y
y = 2² – 2 * 2 + 1
y = 4 – 4 + 1
y = 1 Temos que a equação possui a lei de formação y = x² – 2x +1. E quando x = 2, o valor de y se torna igual a 1.
Resposta Questão 4 No instante em que a parábola cruza o eixo das abscissas o valo de y ou f(x) é igual a zero. Portanto: f(x) = 0
2x² – 3x + 1 = 0
Os pontos de interseção são:
x = 1 e y = 0
x = 1/2 e y = 0
roblema 05. Considere a função f(x) = x2 – 2x + 1. Determine:
a) f(-1) (b) f(1) c) f(-2) d) f(t)
Problema 06. Sabe-se que, sob certo ângulo de tiro, a altura atingida por uma bala, em metros, em função do tempo, em segundos, é dada por h = - 20t2 + 200t. Qual a altura máxima atingida pela bala? Em quanto tempo, após o tiro, a bala atinge a altura máxima?
Resposta
Problema 1.
a) 4 b) 0 c) 9 d) t2– 2t + 1
Problema 3. A bala atinge a altura máxima de 500 m após 5s.
terça-feira, 17 de dezembro de 2013
exercicios.....
Exercícios resolvidos - Funções quadráticas
Hey, você aí que está navegando na net e não encontrou nada de legal para fazer, que tal resolver esses exercícios de matemática?
1- O conjunto-solução da equação q^4 - 13q² + 36 = 0
a) S = {2, 3}
b) S = {0, 2, 3}
c) S = {-3, -2}
d) S = {-3, -2, 2, 3}
2- O número de pontos de intersecção das duas parábolas y = x² e y = 2x² - 1, é:
a) 0
b) 1
c) 2
d) 3
3- Determine o valor de m de modo que a equação 2mx² - (3m + 2)x + 3 = 0 tenha raízes reais e desiguais.
4- (UFRS) A equação 2mx² + mx + 1/2 = 0 possui 2 raízes reais distintas, então:
a) m = 0
b) m > 0
c) m < 4
d) m < 0 ou m > 4
e) 0 < m < 4
5- Na equação 2px² + 3pqx + 3q = 0, a soma das raízes é 9 e o produto é 12. Calcule p + q.
6- A parábola representativa da função f: R -> R, definida por f(x) = -2x² + bx + c, passa pelo ponto (1; 0) e seu ponto de máximo é o ponto B(3; a). Calcule a.
7- (UFPE) O custo C, em reais, para se produzir n unidades de determinado produto é dado por C = 2510 - 100n + n². Quantas unidades deverão ser produzidas para se obter o custo mínimo?
8- (Vunesp) Suponha que um grilo, ao saltar do solo, tenha sua posição no espaço descrita em função do tempo (em segundos) pela expressão h(t) = 3t - 3t², em que h é a altera atingida em metros.
a) Em que instante t o grilo retorna ao solo?
b) Qual a altura áxima em metros atingida pelo grilo?
9- (Udesc) Seja ABCD um quadrado de área unitária, são tomados dois pontos P pertencente a AB e Q pertencente a AD, tais que |AP| + |AQ| = |AD|. Calcule o maior valor para a área do triângulo APQ.
10- (FUVEST) O gráfico de f(x) = x² + bx + c, em que b e c são constantes, passa pelos pontos (0,0) e (1, 2)). Então f(-2/3) vale:
a) -2/9
b) 2/9
c) -1/4
d) 1/4
e) 4
11- Se f(x) = ax² + bx + c com f(2) = 4; f(0) = 2 e f(3) = 14, então a + b + c é igual a:
a) -5
b) -3
c) 0
d) 3
e) 5
Resolução:
1-
Considerando q² = m
m² - 13m + 36 = 0
Bhaskara:
Delta = (13)² - 4(1)(36)
Delta = 169 - 144
Delta = 25
m1 = 13 + 5/2 = 9
m2 = 13 - 5/2 = 4
q² = m1
q² = 9
q = +-3
q² = m2
q² = 4
q - +- 2
S = {-3, -2, 2, 3}
Letra: D
2-
x² = 2x² - 1
x² - 1 = 0
Bhaskara:
Delta = (0)² - 4(1)(-1)
Delta = 4
x1 = +2/2 = 1
x2 = -2/2 = -1
Letra: C
3-
Para que isso ocorre o delta deve ser ≥ 0
Delta1: (3m + 2)² - 4(2m).(3)
Delta1: 9m² + 12m + 4 ≥ 0
Delta2: (12)² - 4(9).(4)
Delta2: 0
m = 12/18
m = 2/3
Resposta: 2/3
4-
2m² + mx + 1/2
Delta = m² - 4(2m).(1/2)
Delta = m² - 4m > 0
Delta2: 16
m1 = 4 + 4/2 = 4
m2 = 4 - 4/2 = 0
Fazendo o estudo dos sinais:
Os valores maior ou igual a zero são:
S = {x e R/ x < 0 ou m > 4}
Letra: B
5-
2px² + 3pqx + 3q = 0
x1 + x2 = -b/a
x1 . x2 = c/a
-3pq = 9
2p
-3q = 18
q = -6
Substituindo em:
3q = 12
2p
3(-6) = 12(2p)
-18 = 24p
p = -3/4
Calculando p + q
-3/4 - 6 = -27/4
Resposta: -27/4
6-
f(x) = - 2x² + bx + c
Xv = -b/2a = 3
(como dito no enunciado, que seu ponto máximo é o ponto (3; 0))
-b/ 2(-2) = 3
b = 12
Sabendo o ponto (1; 0), vamos aplicá-lo na equação:
0 = 2(1)¹ + 12 + c
c = 10
Descobrindo o Yv:
Yv = - (12² - 4.(-2).(-10)) / 4.(-2)
Yv = - (144 - 80)/ -8
Yv = 8
(Esse é o ponto no qual quando x = 3, o y será = 8)
Resposta: a = 8
7-
c = 2² - 100n + 2510
Xv = -b /2a
Xv = 100 / 2
Xv = 50
Resposta: 50 unidades
8-
a) h(t) = -3t² + 3t
h = altura
t = tempo
Xv = -3/ -6
Xv = 1/2 segundo
Como é ida e volta teremos: 1/2 + 1/2 = 1 segundo
b) Yv = (9 - 4(-3.(0)) / 4.(-3)
Yv = 3/4
Yv = 0,75 metro
9-
|AP| + |AQ| = |AD|
ABCD = 1.1 = 1 u
Adotando:
x + y = 1
y = -x + 1
Área(APQ) = x.y / 2
Substituindo y
A = x(-x + 1)/2
A - -x² + x/2
Xv = (-1/2)
2.(-1/2)
Xv = 1/2
y = -1/2 + 1
y = 1/2
Área = (1/2 . 1/2) / 2
Área = 1/8
Resposta: 1/8
10-
f(x) = x² + bx + c
Temos o ponto (0, 0)
Onde:
0² + 0.b + c = 0
c = 0
Temos o ponto (1, 2)
1 + b + c = 2
Como c = 0
1 + b + 0 = 2
b = 1
Substituindo na equação teremos:
f(x) = x² + x
Portanto f(-2/3) vale:
f(-2/3) = (-2/3)² + (-2/3)
f(-2/3) = -2/9
Resposta: -2/9
11-
f(x) = ax² + bx + c
Sabendo que:
f(2) = 4
f(0) = 2
f(3) = 14
I - Substituindo f(2) = 4
4 = a(2)² + b(2) + c
4 = 4a + 2b + c
II - Substituindo f(0) = 2
a(0)² + b(0) + c = 2
c = 2
III - Substituindo f(3) = 14
9a + 3b + c = 14
Ficará então
9a + 3b + 2 = 14
Montando um sistema com a equação I e III temos:
4a + 2b + 2 = 4 (x-3)
9a + 3b + 2 = 14 (x2)
Ficará:
-12 = -12a - 6b - 6
28 = 18a + 6b + 4
16 = 6a - 2
18 = 6a
a = 3
Substituindo na equação I:
4 = 4(3) + 2b + 2
2 = 12 + 2b
-10 = 2b
b = -5
Portanto, a + b + c
3 - 5 + 2 = 0
Letra: C
Espero que tenha ajudado vocês!!
1- O conjunto-solução da equação q^4 - 13q² + 36 = 0
a) S = {2, 3}
b) S = {0, 2, 3}
c) S = {-3, -2}
d) S = {-3, -2, 2, 3}
2- O número de pontos de intersecção das duas parábolas y = x² e y = 2x² - 1, é:
a) 0
b) 1
c) 2
d) 3
3- Determine o valor de m de modo que a equação 2mx² - (3m + 2)x + 3 = 0 tenha raízes reais e desiguais.
4- (UFRS) A equação 2mx² + mx + 1/2 = 0 possui 2 raízes reais distintas, então:
a) m = 0
b) m > 0
c) m < 4
d) m < 0 ou m > 4
e) 0 < m < 4
5- Na equação 2px² + 3pqx + 3q = 0, a soma das raízes é 9 e o produto é 12. Calcule p + q.
6- A parábola representativa da função f: R -> R, definida por f(x) = -2x² + bx + c, passa pelo ponto (1; 0) e seu ponto de máximo é o ponto B(3; a). Calcule a.
7- (UFPE) O custo C, em reais, para se produzir n unidades de determinado produto é dado por C = 2510 - 100n + n². Quantas unidades deverão ser produzidas para se obter o custo mínimo?
8- (Vunesp) Suponha que um grilo, ao saltar do solo, tenha sua posição no espaço descrita em função do tempo (em segundos) pela expressão h(t) = 3t - 3t², em que h é a altera atingida em metros.
a) Em que instante t o grilo retorna ao solo?
b) Qual a altura áxima em metros atingida pelo grilo?
9- (Udesc) Seja ABCD um quadrado de área unitária, são tomados dois pontos P pertencente a AB e Q pertencente a AD, tais que |AP| + |AQ| = |AD|. Calcule o maior valor para a área do triângulo APQ.
10- (FUVEST) O gráfico de f(x) = x² + bx + c, em que b e c são constantes, passa pelos pontos (0,0) e (1, 2)). Então f(-2/3) vale:
a) -2/9
b) 2/9
c) -1/4
d) 1/4
e) 4
11- Se f(x) = ax² + bx + c com f(2) = 4; f(0) = 2 e f(3) = 14, então a + b + c é igual a:
a) -5
b) -3
c) 0
d) 3
e) 5
Resolução:
1-
Considerando q² = m
m² - 13m + 36 = 0
Bhaskara:
Delta = (13)² - 4(1)(36)
Delta = 169 - 144
Delta = 25
m1 = 13 + 5/2 = 9
m2 = 13 - 5/2 = 4
q² = m1
q² = 9
q = +-3
q² = m2
q² = 4
q - +- 2
S = {-3, -2, 2, 3}
Letra: D
2-
x² = 2x² - 1
x² - 1 = 0
Bhaskara:
Delta = (0)² - 4(1)(-1)
Delta = 4
x1 = +2/2 = 1
x2 = -2/2 = -1
Letra: C
3-
Para que isso ocorre o delta deve ser ≥ 0
Delta1: (3m + 2)² - 4(2m).(3)
Delta1: 9m² + 12m + 4 ≥ 0
Delta2: (12)² - 4(9).(4)
Delta2: 0
m = 12/18
m = 2/3
Resposta: 2/3
4-
2m² + mx + 1/2
Delta = m² - 4(2m).(1/2)
Delta = m² - 4m > 0
Delta2: 16
m1 = 4 + 4/2 = 4
m2 = 4 - 4/2 = 0
Fazendo o estudo dos sinais:
Os valores maior ou igual a zero são:
S = {x e R/ x < 0 ou m > 4}
Letra: B
5-
2px² + 3pqx + 3q = 0
x1 + x2 = -b/a
x1 . x2 = c/a
-3pq = 9
2p
-3q = 18
q = -6
Substituindo em:
3q = 12
2p
3(-6) = 12(2p)
-18 = 24p
p = -3/4
Calculando p + q
-3/4 - 6 = -27/4
Resposta: -27/4
6-
f(x) = - 2x² + bx + c
Xv = -b/2a = 3
(como dito no enunciado, que seu ponto máximo é o ponto (3; 0))
-b/ 2(-2) = 3
b = 12
Sabendo o ponto (1; 0), vamos aplicá-lo na equação:
0 = 2(1)¹ + 12 + c
c = 10
Descobrindo o Yv:
Yv = - (12² - 4.(-2).(-10)) / 4.(-2)
Yv = - (144 - 80)/ -8
Yv = 8
(Esse é o ponto no qual quando x = 3, o y será = 8)
Resposta: a = 8
7-
c = 2² - 100n + 2510
Xv = -b /2a
Xv = 100 / 2
Xv = 50
Resposta: 50 unidades
8-
a) h(t) = -3t² + 3t
h = altura
t = tempo
Xv = -3/ -6
Xv = 1/2 segundo
Como é ida e volta teremos: 1/2 + 1/2 = 1 segundo
b) Yv = (9 - 4(-3.(0)) / 4.(-3)
Yv = 3/4
Yv = 0,75 metro
9-
|AP| + |AQ| = |AD|
ABCD = 1.1 = 1 u
Adotando:
x + y = 1
y = -x + 1
Área(APQ) = x.y / 2
Substituindo y
A = x(-x + 1)/2
A - -x² + x/2
Xv = (-1/2)
2.(-1/2)
Xv = 1/2
y = -1/2 + 1
y = 1/2
Área = (1/2 . 1/2) / 2
Área = 1/8
Resposta: 1/8
10-
f(x) = x² + bx + c
Temos o ponto (0, 0)
Onde:
0² + 0.b + c = 0
c = 0
Temos o ponto (1, 2)
1 + b + c = 2
Como c = 0
1 + b + 0 = 2
b = 1
Substituindo na equação teremos:
f(x) = x² + x
Portanto f(-2/3) vale:
f(-2/3) = (-2/3)² + (-2/3)
f(-2/3) = -2/9
Resposta: -2/9
11-
f(x) = ax² + bx + c
Sabendo que:
f(2) = 4
f(0) = 2
f(3) = 14
I - Substituindo f(2) = 4
4 = a(2)² + b(2) + c
4 = 4a + 2b + c
II - Substituindo f(0) = 2
a(0)² + b(0) + c = 2
c = 2
III - Substituindo f(3) = 14
9a + 3b + c = 14
Ficará então
9a + 3b + 2 = 14
Montando um sistema com a equação I e III temos:
4a + 2b + 2 = 4 (x-3)
9a + 3b + 2 = 14 (x2)
Ficará:
-12 = -12a - 6b - 6
28 = 18a + 6b + 4
16 = 6a - 2
18 = 6a
a = 3
Substituindo na equação I:
4 = 4(3) + 2b + 2
2 = 12 + 2b
-10 = 2b
b = -5
Portanto, a + b + c
3 - 5 + 2 = 0
Letra: C
Espero que tenha ajudado vocês!!
introdução a função quadratica
função quadratica.
Definição
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a  0.
0.
Vejamos alguns exemplos de função quadráticas:
Vejamos alguns exemplos de função quadráticas:
- f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
- f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a  0, é uma curva chamadaparábola.
0, é uma curva chamadaparábola.
Exemplo:
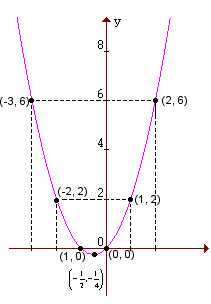
Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
|  |
Observação:
Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
- se a > 0, a parábola tem a concavidade voltada para cima;
- se a < 0, a parábola tem a concavidade voltada para baixo;
Zero e Equação do 2º Grau
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a  0, os números reais x tais que f(x) = 0.
0, os números reais x tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:
Temos:
Observação
A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando 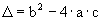 , chamado discriminante, a saber:
, chamado discriminante, a saber:
- quando
 é positivo, há duas raízes reais e distintas;
é positivo, há duas raízes reais e distintas; - quando
 é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais); - quando
 é negativo, não há raiz real.
é negativo, não há raiz real.
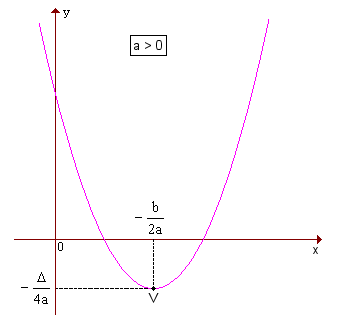
Coordenadas do vértice da parábola
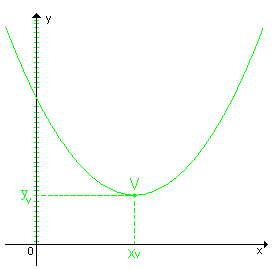
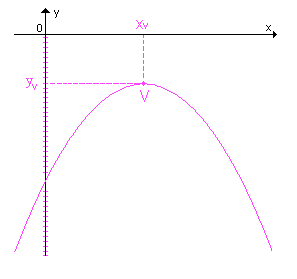
Quando a > 0, a parábola tem concavidade voltada para cima e um ponto de mínimo V; quando a < 0, a parábola tem concavidade voltada para baixo e um ponto de máximo V.
Em qualquer caso, as coordenadas de V são 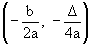 . Veja os gráficos:
. Veja os gráficos:
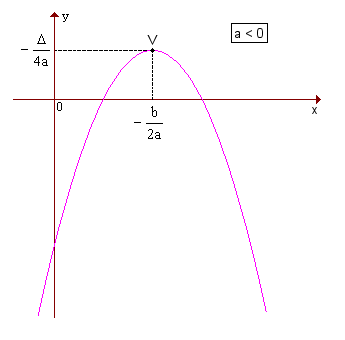
Imagem
O conjunto-imagem Im da função y = ax2 + bx + c, a  0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:
0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:
1ª - quando a > 0,
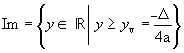
a > 0
|
2ª quando a < 0,
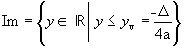
a < 0
|
Construção da Parábola
É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares (x, y), mas seguindo apenas o roteiro de observação seguinte:
Sinal
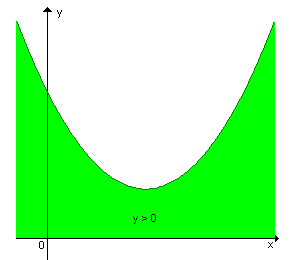
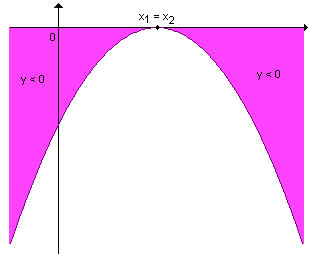
Consideramos uma função quadrática y = f(x) = ax2 + bx + c e determinemos os valores de x para os quais y é negativo e os valores de x para os quais y é positivos.
Conforme o sinal do discriminante
1º -
Nesse caso a função quadrática admite dois zeros reais distintos (x1 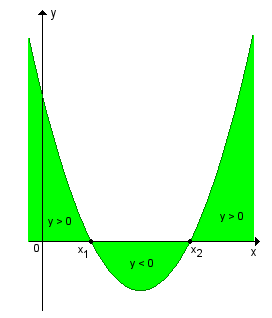
y > 0
y < 0 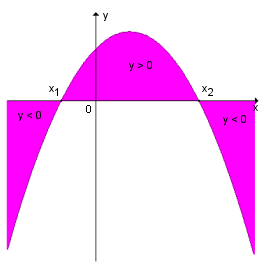
y > 0
y < 0
2º -
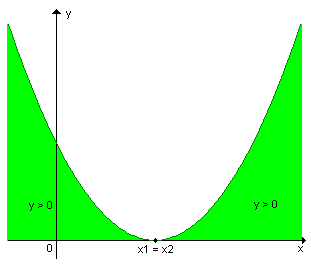
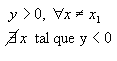 
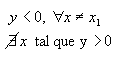
|
Assinar:
Postagens (Atom)