 7) Uma função linear cujos pontos tem abscissa com valor simétrico ao da ordenada, é uma função afim crescente?
7) Uma função linear cujos pontos tem abscissa com valor simétrico ao da ordenada, é uma função afim crescente?
Uma função linear é da forma 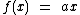 com
com 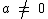 , ou seja, é uma função afim da forma
, ou seja, é uma função afim da forma 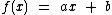 , com
, com 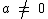 e com
e com 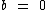 .
.
 Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.
Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.
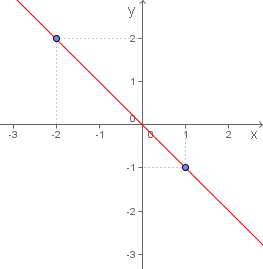
O seu gráfico temos ao lado.
Para obtê-lo escolhemos dois pontos aleatoriamente, segundo a indicação do enunciado e traçamos a reta que os contém.
Obviamente este é o gráfico de uma função decrescente e não de uma função crescente.
Mas você não precisa ter o gráfico para solucionar este problema.
Já que os pontos do gráfico são (x, -x), quando aumentamos o valor de x, consequentemente diminuímos o valor de y que é igual a -x, então tal função é decrescente, pois para ser crescente, ao aumentarmos o valor de x, o valor de y também deveria aumentar.
 Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
 Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.
Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.O seu gráfico temos ao lado.
Para obtê-lo escolhemos dois pontos aleatoriamente, segundo a indicação do enunciado e traçamos a reta que os contém.
Obviamente este é o gráfico de uma função decrescente e não de uma função crescente.
Mas você não precisa ter o gráfico para solucionar este problema.
Já que os pontos do gráfico são (x, -x), quando aumentamos o valor de x, consequentemente diminuímos o valor de y que é igual a -x, então tal função é decrescente, pois para ser crescente, ao aumentarmos o valor de x, o valor de y também deveria aumentar.
 Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
Nenhum comentário:
Postar um comentário