link de videos abaixo .
segunda-feira, 18 de novembro de 2013
video sobre funçao afim.
esses dois videos falam sobre a funçao afim .assistam para poder entender um pouco mais sobre estse assunto. (da aluna carolaine conceiçao).
funçao afim parte 2 (aluna taina karine)
Raiz da Função Afim
Observe no gráfico acima que a reta da função intercepta o eixo das abscissas no ponto (-10, 0).Este valor de x = -10 que leva a y = 0 é denominado raiz da função ou zero da função.
Sendo
Obtendo a Lei de Formação de uma Função Afim a partir de Dois Pontos da Reta
No gráfico acima vemos que o ponto (0, 5) pertence à função, então na sentençaNovamente segundo o gráfico o ponto (-10, 0) também pertence à função e já que b = 5 temos:
Observe que substituímos y, x e b por 0, -10 e 5 respectivamente, obtendo a = 1/2.
Visto que a = 1/2 e b = 5, temos:
Portanto a função
Exatamente como havíamos visto no começo da matéria.
Vale ressaltar que chegaríamos à mesma definição da função, quaisquer que fossem os dois pontos distintos pertencentes a reta exemplo, que utilizássemos na realização dos cálculos.

funçao afim - problema respondido (aluna ana jessica)
 7) Uma função linear cujos pontos tem abscissa com valor simétrico ao da ordenada, é uma função afim crescente?
7) Uma função linear cujos pontos tem abscissa com valor simétrico ao da ordenada, é uma função afim crescente?
Uma função linear é da forma 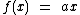 com
com 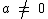 , ou seja, é uma função afim da forma
, ou seja, é uma função afim da forma 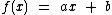 , com
, com 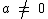 e com
e com 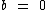 .
.
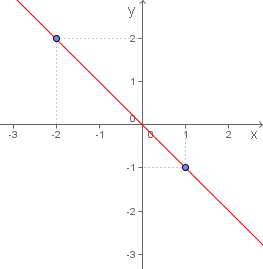 Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.
Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.
O seu gráfico temos ao lado.
Para obtê-lo escolhemos dois pontos aleatoriamente, segundo a indicação do enunciado e traçamos a reta que os contém.
Obviamente este é o gráfico de uma função decrescente e não de uma função crescente.
Mas você não precisa ter o gráfico para solucionar este problema.
Já que os pontos do gráfico são (x, -x), quando aumentamos o valor de x, consequentemente diminuímos o valor de y que é igual a -x, então tal função é decrescente, pois para ser crescente, ao aumentarmos o valor de x, o valor de y também deveria aumentar.
 Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
 Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.
Segundo o enunciado, um determinado ponto desta função linear é identificado por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa x.O seu gráfico temos ao lado.
Para obtê-lo escolhemos dois pontos aleatoriamente, segundo a indicação do enunciado e traçamos a reta que os contém.
Obviamente este é o gráfico de uma função decrescente e não de uma função crescente.
Mas você não precisa ter o gráfico para solucionar este problema.
Já que os pontos do gráfico são (x, -x), quando aumentamos o valor de x, consequentemente diminuímos o valor de y que é igual a -x, então tal função é decrescente, pois para ser crescente, ao aumentarmos o valor de x, o valor de y também deveria aumentar.
 Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente.
Não, embora a função linear com tais características seja uma função afim, ela é uma função decrescente. sábado, 16 de novembro de 2013
* funçao afim*
* uma função definida por f: r -> r chama-se afim quando existem constantes a ,b que pertencem ao conjunto dos reais tais que f (x) ax+b para todo x € r . a lei que define a função afim é : f(x) = ax + b (a € r) * o grafico de uma função afim é uma reta não perpendicular ao eixo ox .
autora : tiala conceiçao.
Assinar:
Postagens (Atom)
